L’autre jour, je me posais une question : comment calculer le volume d’une pyramide ? Oui, je sais, ça peut paraître un peu geek comme interrogation, mais avouez que c’est intrigant. Et puis, entre nous, qui n’a jamais été curieux de savoir combien d’espace prend une de ces grandes structures pointues ? Alors, si ça vous dit, je vous propose qu’on explore ensemble cette question. Pas de panique, je vais tout vous expliquer simplement. Vous êtes partant ? Allez, suivez-moi !
Comment calculer le volume d’une pyramide ? Rien de plus simple avec notre calculatrice
Si l’idée de calculer le volume d’une pyramide vous semble compliquée, détrompez-vous. Avec notre calculatrice, vous aurez une réponse précise en un instant. Oubliez les formules compliquées, nous avons l’outil qu’il vous faut.
Guide d’utilisation de la calculatrice de volume de la pyramide
Saisie des informations
Indiquez les dimensions de votre pyramide : la longueur et la largeur de la base, ainsi que la hauteur. Il est important de rester cohérent en utilisant la même unité de mesure pour chaque dimension.
Comprendre les résultats
Une fois les dimensions renseignées, la calculatrice déterminera et affichera le volume de la pyramide. C’est direct et efficace.
Recommandations
Pour mesurer avec précision, n’hésitez pas à utiliser un mètre ruban ou une règle graduée. Et un petit conseil : si vous optez pour une autre unité de mesure, pensez à ajuster toutes les dimensions en conséquence.
Dans cet article, vous trouverez
La formule du volume d’une pyramide expliquée simplement
Pour commencer, qu’est-ce au juste qu’une pyramide ?

Un machin avec des triangles de chaque côté ? Mouais… On sait tous ce qu’est une pyramide (à peu près en tout cas) mais comment la définir mathématiquement ?
Une pyramide est une forme solide qui a une base plate et des faces inclinées qui se rejoignent en un point appelé le sommet. Imaginez une tente de camping : le sol serait la base et les côtés de la tente qui se rejoignent en haut seraient les faces inclinées de la pyramide. Le point le plus haut de la tente, là où tous les côtés se rencontrent, c’est le sommet de la pyramide.
La base peut être de différentes formes, comme un carré, un rectangle ou même un triangle ou un pentagone (si si, ça existe), mais les faces inclinées se rejoignent toujours en un seul point au sommet.
Importance culturelle et historique des pyramides
Les pyramides ne sont pas seulement des prouesses architecturales ; elles sont aussi le reflet de la grandeur des civilisations qui les ont érigées. En Égypte, elles symbolisaient l’ascension du pharaon vers les dieux et servaient de tombeaux. Dans d’autres cultures, comme chez les Mayas, elles avaient des fonctions religieuses et cérémonielles. Ces structures majestueuses témoignent de l’ingéniosité humaine et de la quête éternelle de l’immortalité.
Comment calculer le volume d’une pyramide manuellement ? Grâce à la formule du volume d’une pyramide !
Il y a un truc amusant avec les pyramides, ou plus généralement avec les « trucs pointus » (les cônes par exemple) : la formule du volume d’une pyramide est la même quelle que soit la forme de base. Carré, rectangle, triangle, rond, peu importe, c’est toujours la même formule !
Le volume d’une pyramide dépend uniquement de sa base et de sa hauteur.
La formule du volume d’une pyramide est :
V = 1/3 x aire de la base de la pyramide × hauteur de la pyramide
Hauteur ok, mais QUELLE hauteur ? Une pyramide a trois types de hauteurs….
– La hauteur principale, celle dont on parle dans la formule de calcul du volume d’une pyramide, est celle qui part du sommet pour rejoindre le centre de la base.
– il y a aussi les hauteurs des faces, qui débutent également au sommet mais se terminent au milieu de l’un des côtés de la base
– enfin il y a ce que l’on pourrait appeler les « hauteurs latérales », qui sont en fait les arêtes qui relient le sommet aux sommets de la base.
Mais pour calculer le volume d’une pyramide, c’est bien la première hauteur, celle qui va du sommet jusqu’au centre de la base, qui est prise en compte.
Quelques cas particuliers de calcul du volume d’une pyramide
Pyramide à base rectangulaire
Si la base est un rectangle de longueur l et de largeur L, l’aire de la base est l×L. Donc le calcul du volume d’une pyramide devient l x L x H / 3
Exemple : Pour une pyramide ayant une base de 3 mètres de longueur et 2 mètres de largeur, avec une hauteur de 4 mètres, le volume serait V=1/3 × 3 × 2 × 4=8 mètres cubes.
Pyramide à base carrée
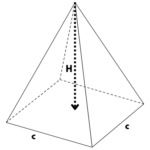
Si la base est un carré de côté c, l’aire de la base est c2.
Exemple : Pour une pyramide de base carrée de 3 mètres de côté et de 4 mètres de hauteur, le volume serait V = 1/3×32×4=12 mètres cubes.
Pyramide à base triangulaire
Si la base est un triangle de base b et de hauteur ℎ, l’aire de la base est 1/2×ℎ×b et donc le volume de la pyramide devient : 1/2 x h x b x H x 1/3 soit 1/6 x hauteur du triangle x base du triangle x Hauteur de la pyramide.
Exemple : Pour une pyramide à base triangulaire avec une base de 3 mètres, une hauteur de triangle de 2 mètres et une hauteur de pyramide de 4 mètres, le volume serait V=1/3×1/2×3×2×4=8 mètres cubes.
Cône (cas particulier de pyramide)
Et oui c’est surprenant mais un cône est en réalité une pyramide … ronde ! Il obéit donc aux mêmes lois mathématiques de calcul du volume
Si la base est un cercle de rayon r, l’aire de la base est π x r2 et donc le calcul devient π x r2 x 1/3 x H.
Exemple : Pour un cône de 3 mètres de rayon et de 4 mètres de hauteur, le volume serait V=1/3×π×32×4≈37.7 mètres cubes.
Démonstration de la formule de calcul du volume d’une pyramide
La raison pour laquelle nous multiplions par 1/3 vient de la géométrie. Imaginez une pyramide à l’intérieur d’un prisme droit (ou un cylindre pour un cône) ayant la même hauteur et la même aire de base. La pyramide ne remplira que le tiers du volume du prisme droit (ou du volume du cylindre pour un cône). D’où le facteur 1/3.
Relation avec d’autres formes géométriques
La pyramide a des relations intéressantes avec d’autres solides.
Par exemple, si vous comparez un prisme et une pyramide ayant la même base et la même hauteur, le volume du prisme droit est toujours égal à 3 fois celui de la pyramide.
De même, un cône peut être vu comme une pyramide dont la base est un cercle. La formule pour le calcul du volume d’un cône est analogue à celle de la pyramide, où l’aire de la base est multipliée par la hauteur.
A quoi ça sert de calculer le volume d’une pyramide ?
Maintenant, vous vous demandez peut-être : « Pourquoi aurais-je besoin de savoir comment calculer le volume d’une pyramide ? »
Bon va être honnête, dans la vie courante, à pas grand chose sauf à satisfaire votre curiosité si vous voyagez en Egypte et souhaitez calculer le poids des pyramides 😅.
Mais si vous êtes architecte, ingénieur ou même étudiant, cela pourrait vous être utile un jour. Et puis, c’est toujours intéressant de savoir comment les choses fonctionnent, non ?
Anecdotes et pyramides célèbres
Parlons un peu des pyramides célèbres. La Grande Pyramide de Gizeh, par exemple, a un volume impressionnant d’environ 2,5 millions de mètres cubes. Le volume de la pyramide de Khufu (ou Kheops) est de 2,4 millions de m³
Mais la plus grande pyramide, et également le plus grand monument jamais construit, n’est pas en Egypte ! C’est la Pyramide de Quetzalcóatl à Cholula de Rivadavia, située à 101 km au sud-est de Mexico City. Elle mesure 54 mètres de haut, et sa base couvre une superficie de près de 18,2 hectares. Son volume total est estimé à 3,3 millions de m³ !
Records amusants de pyramides
Le livre Guinness des records cite un certain nombre de pyramides amusantes
Pyramide de sucre : Paul Van Den a construit la plus grande pyramide de cubes de sucre, composée de 10.416 cubes. Imaginez combien de tasses de café vous pourriez sucrer avec ça !
Pyramide de machines à laver : Currys et Ainscough Training ont établi le record de la plus grande pyramide de machines à laver, avec 1.496 machines empilées. Espérons qu’aucune n’était en marche !
Pyramide humaine sur moto : L’équipe Dare Devils de l’Indian Army Signal Corps a réalisé une pyramide de moto avec 201 personnes. C’est un sacré équilibre !
Pyramide de canettes : Transmed Overseas et Pringles ont créé la plus grande pyramide de canettes, composée de 31.001 canettes. Espérons qu’ils n’aient pas eu soif pendant la construction !
Pyramide de pièces : Vytautas Jakštas et Domas ont construit la plus grande pyramide de pièces, composée de 1.000.935 pièces. C’est une façon originale d’économiser !
Pyramide de balles de golf : Zachary Krivda a établi le record de la plus grande pyramide de balles de golf, avec 17.575 balles. Espérons qu’il n’y avait pas de vent ce jour-là !
Pyramide de rouleaux de papier toilette : Elleair International a établi le record de la plus haute pyramide de rouleaux de papier toilette, mesurant 4.539 m. C’est une réserve pour combien de temps ?
Pyramide de caisses de bière : Quandt-Schön a construit la plus grande pyramide de caisses de bière, composée de 105.995 caisses. Une pyramide qui donne soif !
Pyramide humaine sous-marine : Tyler Reiser, Manolo et leur équipe ont établi le record de la plus grande pyramide humaine sous-marine, avec 62 personnes. Espérons qu’ils aient tous eu des tubas !
Pyramide de cookies : et voilà enfin la pyramide la plus gourmande ! Le record de la plus haute pyramide de biscuits a été établi à 1,49 mètre. Ce record a été réalisé par Jan Vinzenz Krause et des membres du diocèse d’Essen, en utilisant 12 180 biscuits au beurre Leibniz. On aurait bien aimé calculer le volume de cette pyramide de cookies, pour savoir combien de gourmands ont pu se régaler 😋
Vos questions, nos réponses sur le volume des pyramides
Peut-on calculer le volume d’un triangle ?
Non, un triangle est une figure bidimensionnelle, donc il n’a pas de volume. On ne peut pas faire le calcul du volume du triangle.
Cependant, on peut calculer l’aire d’un triangle. Si vous pensez au volume d’une forme tridimensionnelle avec une base triangulaire, vous faites probablement référence à une pyramide à base rectangulaire ou au volume d’un prisme droit. Ca tombe bien, pour calculer le volume d’une pyramide, vous avez tout ce qu’il faut ci-dessus 😉
Quelle est la différence entre une pyramide et un prisme ?
La principale distinction se trouve dans leurs bases et leurs sommets. Une pyramide a une base et un sommet unique, tandis qu’un prisme possède deux bases parallèles et identiques. Le volume d’une pyramide équivalant à un tiers de celui d’un prisme ayant la même base et la même hauteur, la pyramide est donc moins « volumineuse ».
Comment calcule-t-on le volume d’une pyramide à base circulaire ?
Une pyramide à base circulaire est en réalité un cône 😊.
Pour calculer son volume, on utilise la formule : V = 1/3 × π × r2 × h, où r est le rayon de la base et h est la hauteur du cône.
Est-ce que toutes les pyramides ont une base triangulaire ?
Non, une pyramide est définie par sa base et son sommet unique. Cette base peut avoir n’importe quelle forme : triangle, carré, rectangle, pentagone, etc.
Qu’est-ce qu’une pyramide oblique ?
Contrairement à une pyramide régulière, où les faces latérales convergent symétriquement vers le sommet, dans une pyramide oblique, les faces latérales sont inclinées de manière asymétrique. Le volume d’une pyramide oblique est le même que celui d’une pyramide régulière ayant la même base et la même hauteur.
Comment trouver la hauteur d’une pyramide ?
Si vous connaissez le volume de la pyramide et la superficie de sa base, vous pouvez utiliser ces informations pour trouver sa hauteur. Prenons la formule du volume d’une pyramide : Volume = (1/3) * superficie de la base * hauteur.
Si vous avez le volume et la superficie de la base, vous pouvez réorganiser cette formule pour avoir : Hauteur = (3 * Volume) / superficie de la base.
Comment calculer le volume d’une pyramide tronquée ?
Une pyramide tronquée est comme une pyramide normale, mais on lui a coupé le sommet. Pour trouver son volume, imaginez que vous avez deux pyramides : la grande pyramide d’origine et la petite pyramide coupée du sommet. Le volume de la pyramide tronquée est la différence entre ces deux volumes.
La formule pour le volume d’une pyramide tronquée est : Volume = (1/3) * Hauteur de la pyramide tronquée * (superficie de la grande base + superficie de la petite base + racine carrée de (superficie de la grande base * superficie de la petite base)).